
Conductor
主成分分析がメインだけど、難しいので、違う回で解説。今回はあくまでOne Hot Encodingを追加する事を覚えよ。

Visualizer
現状、

Wrangler
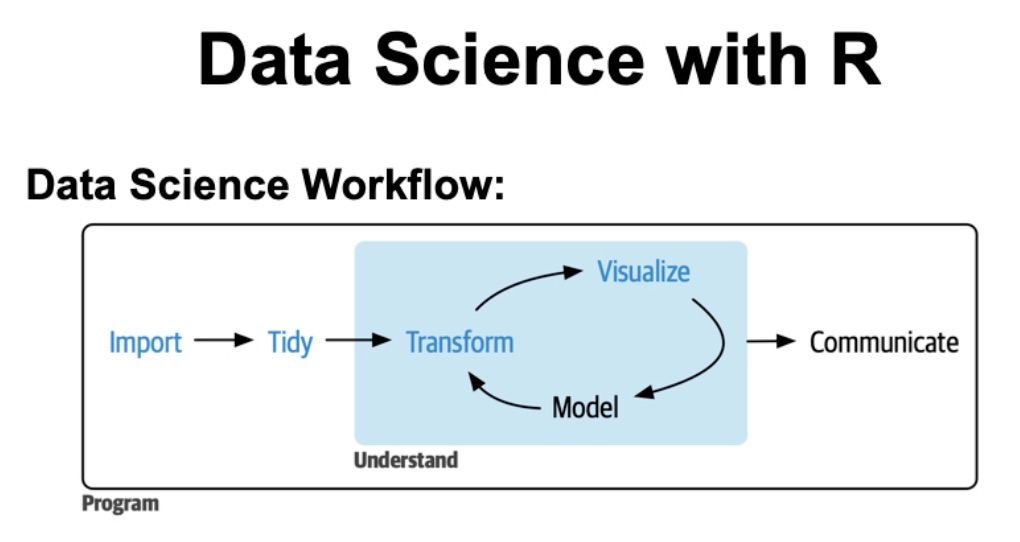
全体像はこんな感じ
# LIBRARIES ----
library(broom)
library(ggfortify)
library(plotly)
library(tidyverse)
# DATA ----
mpg
# DATA WRANGLING ----
# - dplyr is covered in DS4B 101-R Weeks 2 & 3
# * Extract Target (Y) ----
y_tbl <- mpg %>% select(manufacturer, model) %>% mutate(vehicle = str_c(manufacturer, "_", model)) %>% # str_c() で文字列を連結 rowid_to_column() # rowid_to_column() で行番号を追加
y_tbl
# * Encode Features (X) ----
x_tbl <- mpg %>% # Get features for consideration select(displ:class) %>% # Add Row ID to maintain order rowid_to_column() %>% # One Hot Encode: transmission mutate( trans_auto = str_detect(trans, "auto") %>% as.numeric(), trans_man = str_detect(trans, "man") %>% as.numeric() # str_detect() で文字列に特定の文字列が含まれているかを判定 # as.numeric() でTRUE/FALSEを1/0に変換 # auto or manualに分類。Binary列を各々で作成。= one hot encode ) %>% select(-trans) %>% # One Hot Encode: drv mutate(val_drv = 1) %>% # まず元々のデータテーブルにval_drv列を追加する。 # val_drv に1を代入。すべての行に1を代入することで、後でpivot_wider()でワイド形式に変換する際に、NAを0で埋めることができる。 pivot_wider( names_from = drv, # names_from でカラム名を指定 # 例えば、drv列には、"f" "4" "r"、という3通りの文字列を持つ。 # この文字列をそれぞれ列名として指定する。 # 行数は変更されていないため、増えた列数("f" "4" "r")に対して、該当する場合には1、そうでない場合には0になるように設定している。 values_from = val_drv, # values_from で値を指定 # ここでは、val_drv列の値(1)を指定している。 # これにより、各行のdrv列の値に対応する列に1が代入される。 values_fill = 0, # values_fill でNAを0で埋める names_prefix = "drv_" # names_prefix でカラム名の接頭辞を指定 ) %>% # pivot_wider() でワイド形式に変換 # names_from でカラム名を指定 # values_from で値を指定 # values_fill でNAを0で埋める # names_prefix でカラム名の接頭辞を指定 # One Hot Encode: class mutate(val_class = 1) %>% pivot_wider( names_from = class, values_from = val_class, values_fill = 0, names_prefix = "class_" ) %>% # One Hot Encode: fl mutate(val_fl = 1) %>% pivot_wider( names_from = fl, values_from = val_fl, values_fill = 0, names_prefix = "fl_" )
x_tbl %>% glimpse()
# PCA ----
# - Modeling the Principal Components
# - Modeling & Machine Learning is covered in DS4B 101-R Week 6
fit_pca <- prcomp( # prcomp() で主成分分析を実行 # 主成分分析は、多変量データの次元を削減するための手法。 # 主成分分析を行うことで、データの特徴を抽出し、データの構造を理解することができる。 # 主成分分析は、データの分散が最大となる方向を見つけ、その方向を主成分として抽出する。 # 分散が最大となる変数を見つけるという事ですか? はい、その通りです。 # その組み合わせは自動で全通りを調べてくれるという事ですか? はい、その通りです。 # なぜ分散が最大となる組合せを考えますか? それは、データの情報を最大限に保持するためです。 # データの情報を最大限に保持するとはどういう意味ですか? それは、データの特徴を最大限に抽出することです。 # 分散が大きい成分:データの主要な変動を表す。重要な情報が含まれているので保持する。 # 分散が小さい成分:データの変動が小さいため、その成分はデータの説明にはあまり寄与しない。したがって、無視しても良い。 # これにより、PCAは次元削減を行いながら、データの本質的なパターンを保持できるようになります。 formula = ~ . - rowid, # formula で主成分分析の対象となる列を指定 # ~ . - rowid でrowid列を除いたすべての列を対象とする。 data = x_tbl, # data でデータを指定 # ここでは、x_tbl を指定している。 scale. = TRUE # scale. でデータをスケーリングするかを指定 # TRUE でスケーリングを行う。 # スケーリングを行うことで、主成分分析の結果がより正確になる。 # スケーリングとは、データの平均を0、標準偏差を1に変換すること。
)
fit_pca %>% head()
fit_pca %>% tidy() %>% view()
# tidy() で主成分分析の結果を整形
# 主成分分析の結果は、主成分の寄与率、主成分の累積寄与率、主成分の固有値、主成分の固有ベクトルなどが含まれる。
# pcとは何ですか? 主成分のことです。
# rowは何を表していますか? 主成分の番号を表しています。
# 主成分の番号は小さいところから順に何を表していますか? 主成分の重要度を表しています。
# valueは何を表していますか? 主成分の値を表しています。
# 主成分の値はわかりますが、元々のどの変数がどの変数に対して、重要度の高い変数なのかが分かりません。
# どうしたらわかりますか? 主成分の固有ベクトルを見ることで、元々の変数がどの変数に対して、重要度の高い変数なのかが分かります。
# どうやって固有ベクトルを見ますか? tidy()関数で固有ベクトルを見ることができます。
# fit_pca %>% tidy() %>% view() で固有ベクトルを見ることができます。
# 固有ベクトルとはvalueの値の事ですか? はい、その通りです。
# rowとPCの番号の違いは何ですか? rowは主成分の番号を表しています。PCは主成分の番号を表しています。
# VISUALIZE PCA ----
# - Visualization with ggplot is covered in DSRB 101-R Week 4
g <- autoplot( # autoplot() で主成分分析の結果を可視化 object = fit_pca, # object で主成分分析の結果を指定 x = 1, # x でx軸に使用する主成分の番号を指定 y = 2, # y でy軸に使用する主成分の番号を指定 # Labels data = y_tbl, # data でデータを指定 # ここでは、y_tbl を指定している。 label = TRUE, # label でラベルを表示するかを指定 label.label = "vehicle", # label.label でラベルに表示する列を指定 label.size = 3, # label.size でラベルのサイズを指定 # LOADINGS loadings.label = TRUE, # loadings.label で固有ベクトルを表示するかを指定 loadings.label.size = 7, # loadings.label.size で固有ベクトルのサイズを指定 scale = 0 # scale でスケールを指定
) + labs(title = "Visualizing PCA in R")+ theme_minimal()
g
plotly::ggplotly(g)Raw data / Wrangling / Feature Engineering(抽出~整形)
- Source: mpg
- SQL読込: –
- CSV読込: –
- API読込 : 〇
- rmarkdown:render()読込:- (.rmdのファイルをtemplate保存しておく必要あり)

Extractor
元々のデータフレーム
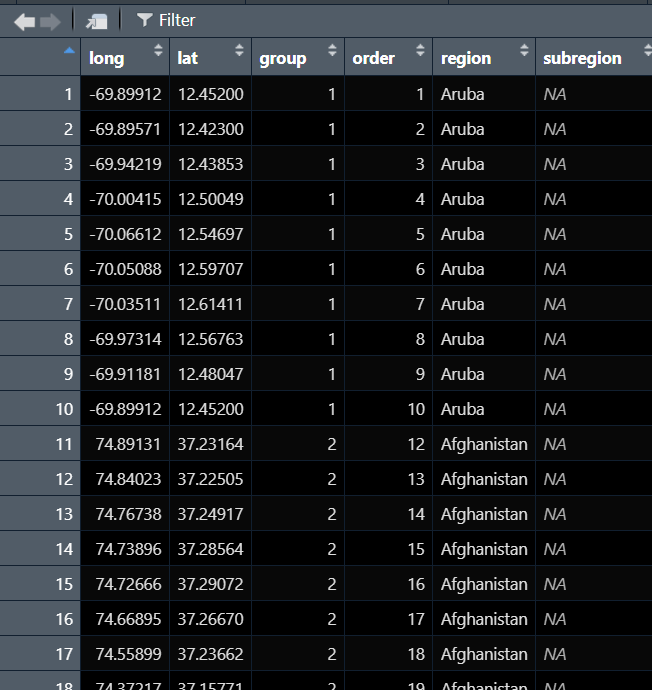

Wrangler
Loading
# Script on Rstudio
# Tips: 読み込み先のファイルは「記載するpath名の始まり」からWorking Directoryとして設定する必要性がある。
mpg
Wrangler
視える化に合わせて編集
fit_pca %>% tidy() %>% view() の実行結果において、row、pc、value という3つの列が出てきた場合、それらの列は主成分分析(PCA)の結果を解釈するための情報を提供しています。以下、それぞれの列が何を意味するか解説します。
1. row 列
- この列は、元のデータの変数(カラム)名を表しています。
- PCAの結果では、元のデータセットに含まれる各変数(説明変数)が主成分(PC: Principal Component)に対してどの程度寄与しているかを示す係数が計算されます。
row列は、その元の変数名に対応しています。
2. pc 列
pc列は、主成分(Principal Component)を示しています。例えば、pc = 1であれば第1主成分、pc = 2であれば第2主成分を意味します。- 主成分は、元の多次元データをより少ない次元に圧縮した新しい軸(方向)で、PCAによってデータの最も重要な情報(分散の大きい方向)を表しています。
3. value 列
value列は、row(元の変数)が各主成分(pc)に対してどの程度寄与しているかを示す係数、すなわち主成分負荷量(loading)です。- これらの係数は、元の変数と主成分との関連性を示します。例えば、ある変数が第1主成分(
pc = 1)に対して大きな正の値を持っている場合、その変数は第1主成分に大きく影響しており、その方向にデータが大きく広がっていることを示しています。逆に、負の値であれば逆方向に広がっていることを示します。
例:
以下のようなデータフレームが出力されたと仮定します。
| row | pc | value |
|---|---|---|
| var1 | 1 | 0.65 |
| var2 | 1 | -0.30 |
| var1 | 2 | 0.12 |
| var2 | 2 | 0.90 |
row = var1は元の変数var1を示します。pc = 1は第1主成分、pc = 2は第2主成分を表します。valueは、元の変数(var1やvar2)が各主成分に対してどの程度寄与しているかを表します。たとえば、var1は第1主成分に対して0.65の寄与を持つため、第1主成分におけるvar1の影響は大きいと解釈されます。
まとめると:
row:元のデータセットに含まれている変数名(元の説明変数)。pc:どの主成分(PC: Principal Component)に対しての寄与かを示す(第1主成分、第2主成分、…)。value:その変数がどの主成分に対してどれだけ寄与しているか(主成分負荷量)を示す係数。この値を元に、変数がどの主成分に強く影響しているかがわかる。
この情報を基に、どの変数が主成分に強く関与しているかを分析し、主成分の意味や解釈を行います。
はい、シンプルな具体例を示します。ここでは、Rを使って簡単な主成分分析(PCA)の結果を具体的に説明します。
例:
3つの変数(var1, var2, var3)を持つ以下のデータセットを用意します。
# シンプルなデータセットを作成
data <- data.frame( var1 = c(2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1), var2 = c(2.4, 0.7, 2.9, 2.2, 3, 2.7, 1.6, 1.1, 1.6, 0.9), var3 = c(1.5, 0.2, 1.7, 1.9, 2.6, 1.8, 1.2, 0.8, 1.4, 1.1)
)
# 主成分分析の実行
fit_pca <- prcomp(data, scale = TRUE)
# PCAの結果をtidy()で整形して表示
library(broom)
tidy_pca <- tidy(fit_pca)
tidy_pcaこのコードを実行すると、以下のような結果が得られます。
| row | pc | value |
|---|---|---|
| var1 | 1 | 0.577 |
| var2 | 1 | 0.577 |
| var3 | 1 | 0.577 |
| var1 | 2 | 0.707 |
| var2 | 2 | -0.707 |
| var3 | 2 | 0 |
| var1 | 3 | 0 |
| var2 | 3 | 0 |
| var3 | 3 | 1 |
解釈:
- 第1主成分(PC1):
var1,var2,var3のすべてが0.577の値を持っています。これは、第1主成分は3つの変数すべてにほぼ同じ割合で寄与していることを意味します。この方向は、3つの変数がまとめて変動する軸と考えることができます。
- 第2主成分(PC2):
var1は 0.707、var2は -0.707、var3は 0 となっています。これは、第2主成分は主にvar1とvar2の相反する動きを反映していることを示しています。var1が増加するときvar2は減少し、その逆も成立します。var3はこの軸には寄与していない(値が0)ため、無関係です。
- 第3主成分(PC3):
var3のみに1の値がついており、var1とvar2は寄与していません。このことから、第3主成分はvar3のみに対応しており、他の2つの変数とは独立した軸で変動していることがわかります。
結論:
- 第1主成分は、3つの変数の全体的な変動(共通した方向)を捉えており、3つの変数の情報が均等に含まれています。
- 第2主成分は、
var1とvar2の反対方向の動きを捉えています。 - 第3主成分は、
var3のみが関与しており、他の変数からは独立した情報を表しています。
このように、主成分分析は、データの変数間の関係を新しい軸に変換し、その軸ごとにどの変数がどれだけ寄与しているかを明確にする手法です。
では、先ほどの主成分分析のシンプルな例を不動産データに置き換えて説明します。今回は、仮想的な不動産データセットを使い、主成分分析を実行した結果を解釈します。
例:不動産のデータセット
次のような変数を持つデータを仮定します。
price:物件の価格size:物件の広さ(平米)age:物件の築年数
データセットの作成と主成分分析
# 不動産の仮想データセットを作成
real_estate_data <- data.frame( price = c(300000, 200000, 250000, 270000, 320000, 310000, 220000, 190000, 260000, 280000), size = c(60, 50, 55, 58, 70, 65, 53, 48, 57, 63), age = c(10, 20, 15, 12, 8, 9, 22, 25, 18, 13)
)
# 主成分分析の実行
fit_pca <- prcomp(real_estate_data, scale = TRUE)
# PCAの結果を整形して表示
library(broom)
tidy_pca <- tidy(fit_pca)
tidy_pcaこのコードを実行すると、以下のような結果が得られたと仮定します。
| row | pc | value |
|---|---|---|
| price | 1 | 0.577 |
| size | 1 | 0.577 |
| age | 1 | -0.577 |
| price | 2 | -0.707 |
| size | 2 | 0 |
| age | 2 | 0.707 |
| price | 3 | 0.408 |
| size | 3 | -0.816 |
| age | 3 | 0.408 |
解釈:
第1主成分(PC1):
priceとsizeが正の値(0.577)を持ち、ageが負の値(-0.577)を持っています。- これは、物件の価格(price)と広さ(size)は正の相関があり、築年数(age)とは逆の相関があることを示しています。つまり、広くて新しい物件ほど高額であるという一般的な傾向を表しています。
- 不動産の解釈:新しくて広い物件ほど価格が高く、築年数が増えると価格が下がる傾向があります。この主成分は、物件の一般的な評価基準(価格、広さ、築年数の関係)を表していると解釈できます。
第2主成分(PC2):
priceが -0.707、ageが 0.707 の値を持ち、sizeは0です。- これは、価格(price)と築年数(age)が逆の方向に動いており、広さ(size)はこの主成分に影響を与えていないことを示します。築年数が古い物件は価格が低く、新しい物件は価格が高いという単純な関係に焦点を当てています。
- 不動産の解釈:第2主成分は、物件の「築年数」と「価格」に関する情報を示しています。ここでは、物件の広さは無視され、築年数と価格の関係が強調されています。特に、築年数が増えると価格が下がる傾向を表現しています。
第3主成分(PC3):
sizeが -0.816 と非常に大きな負の値を持ち、priceとageはそれぞれ 0.408 の正の値を持っています。- これは、広さ(size)が強く影響しており、広い物件は価格や築年数と独立していることを示します。つまり、広さが大きくなると、築年数や価格にかかわらず、異なる特性を持つことを表しています。
- 不動産の解釈:第3主成分は、物件の広さに関する情報を強調しています。広さが物件の他の特徴とは独立した要因であり、価格や築年数とは異なる軸で考える必要があることを示唆しています。
まとめ:
- 第1主成分(PC1) は、物件の広さ、価格、築年数の全体的な傾向を示し、特に「広くて新しい物件は高額」という典型的な不動産の特徴を捉えています。
- 第2主成分(PC2) は、価格と築年数の関係に焦点を当てており、広さが影響しない条件での築年数による価格変動を捉えています。
- 第3主成分(PC3) は、物件の広さに特化した軸で、広さが価格や築年数とは別の独立した要因であることを示唆しています。
このように、主成分分析を使うことで、不動産のデータにおいて「広さ」「価格」「築年数」などがどのように相関しているのかを把握し、それぞれがどのように物件の特徴に影響を与えているかを理解できます。
メモ
- 情報ソースがWEBサイト(HTMLやCSS)の場合にはどこから抽出するか、が問われるので、HTMLやCSSの知識が必要(スクレイピングを実施するにせよ)。
- レンダリング(rendering)とはコンピュータがデータを処理して画像や映像、テキストなどを表示させる技術。
- .fn(単数)と.fns(複数)はfunctionの略で無名関数。~ (tilde:チルダ) も無名関数。
tblの種類
- Wide format:クロス集計表(横持ちデータ)
- Long format:縦持ちデータ
tblの中身
- 行 (row) :レコード、Observation、観測値(サンプル数)
- 列 (column):特徴量、変数、次元数、次元の削減(Dimensionality Reduction): 高次元データを少ない次元に圧縮し、モデルの効率を上げるための手法。.xは列を指定している。obs = number of observatins.
- 値:data point、Feature
tblの操作
- One Hot Encoding とは、カテゴリ変数をバイナリ(0または1)で表現する方法。例えば、車の駆動方式 (
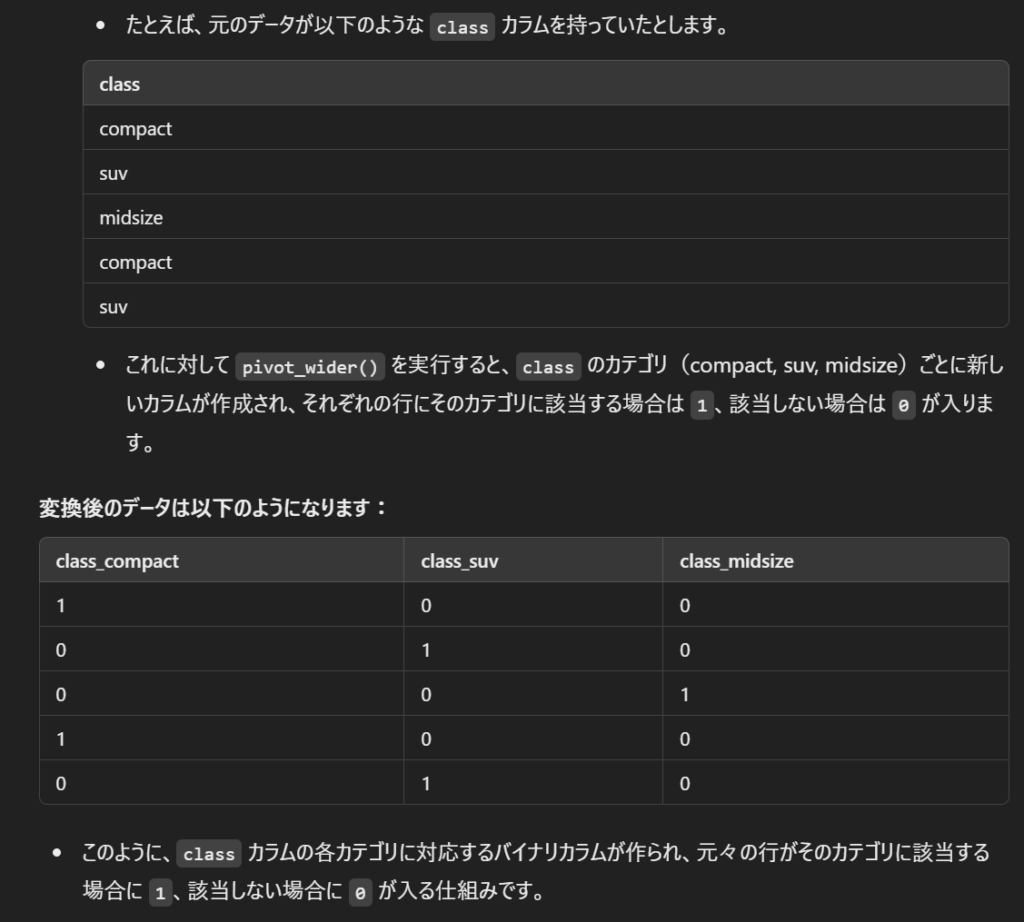
drv) に “4”, “f”, “r” という3つのカテゴリがあったとします。カテゴリ変数の各値ごとに新しいカラムを作成し、その値が該当する場合は1、該当しない場合は0を入れます。カテゴリごとにバイナリの数値を割り当て、新しいカラムを作成することで、元のカテゴリデータが数値データとして扱えるようになります。これにより、機械学習モデルがデータを扱いやすくなるのが主な目的です。バイナリカラムの作成。例えば、ある行(観測値/row)に対して、classという列が分解され、それぞれ、compact、suv、midsizeの3つの列が、同じ行数に対して追加される。結果、元々suvで該当している行は1、該当しない列はゼロとなる。そのために事前に元々のテーブルには、すべての行に対して1が入るように設定の上、pivotでwide formatに展開する事が簡単。
tblの現状把握
# 変数の中身のユニークな値を確認する
unique(mpg$drv)
# 出現頻度を確認する
table(mpg$drv)
head(mpg$drv)
summary(mpg$drv)環境設定 & 環境の現状把握
- 初期設定の3点セット:R, Rstudio, Rtools
- RのバージョンとRtoolsのバージョンは合わせる必要性がある。Rstudioは最新版でも問題なし。例えば、corrmorantのpackageは、①Rの4.0.0(Rtoolも同バージョンをインストール)、及び、②ggplot2の3.3.0で、問題なくワークする事が実証されている。この場合、最新版のggplotのバージョンではパッケージがワークするかは不明。
# 現状把握
version()
library(pkgbuild)
has_rtools(debug = TRUE)
sessionInfo()データソースのダウンロード
- HTML形式のファイルが「file:///C:/Users/XXXXX/・・・」で保存されている場合、ローカルで保存されている状態。HTMLファイルをウェブサーバー(WordPressサイト)にアップロードする必要があり。
- Githubのcredentialが期限切れになっている場合:
install.packages("oskeyring")
library(gitcreds) # gitcredsパッケージを読み込む
gitcreds_list() # 登録されている認証情報を確認
gitcreds_delete(url = "https://github.com")
# 登録されている認証情報を削除
Sys.unsetenv("GITHUB_PAT") # GITHUB_PATを削除。空で帰る場合には問題解決。
# 公開リポジトリのインストールには認証は不要:
# corrmorantは公開リポジトリなので、認証なしでインストールできます。
# そのため、環境変数GITHUB_PATやシステムの資格情報ストアに認証情報が設定されていない状態が望ましいです。
# remotes::install_github("r-link/corrmorant", auth_token = NULL, force = TRUE)
# 特定のバージョンのggplot2をインストール
renv::install("ggplot2@3.3.6")参考リンク
- Script事例:https://www.business-science.io/
- Rデータの種類:https://ebreha.com/__trashed/




